投資を始めるか悩むポイントの一つに、投資の結果が不確定なことがあると思います。「大きく損をしたらどうしよう」と不安に思っている方も多いのではないでしょうか。
そんな不安がある方には、投資結果をシミュレーションする方法を学ぶことがおすすめ。この記事では、投資結果のシミュレーション方法や、実践的に投資が学べるゲームなどを紹介します。
まずは投資の鍵となる「複利」を理解しよう
投資を理解するうえで欠かせないのが、金融商品の運用方法の一つである「複利」を理解することです。金融商品の運用方式には複利と単利があり、多くの投資商品が複利で運用されています。単利と複利の概要は以下のとおりです。
- 単利:元本から発生した運用益を元本に加えずに運用し続ける方法
- 複利:元本から発生した運用益を元本に加えながら運用し続ける方法
例えば、100万円を年利1%で運用した場合、単利運用だと何年たっても元本は100万円のままですが、複利の場合は、元本が2年目に101万円、3年目に102.01万円と徐々に増えていきます。また、元本が増えるに伴って運用益も増えていきます。
複利の計算ができるようになると、投資信託の平均利回りを使って見込まれる利益を予想できるようになりますし、固定金利の国債のように利回りが固定されている商品であれば、将来得られる正確な額を算出できるようになります。
複利の計算方法
複利の計算方法は以下のとおりです。
- 元本×(1+利率)^n
n=運用に要する年数
例:元本100万円を5年間、1%で運用した場合
- 計算式:1,000,000×(1+0.01)^n
- 1年目:1,000,000×(1+0.01)^1=1,010,000…年間運用益:1万円
- 2年目:1,010,000×(1+0.01)^1=1,020,100…年間運用益:1万100円
- 3年目:1,020,100×(1+0.01)^1=1,030,301…年間運用益:1万201円
- 4年目:1,030,301×(1+0.01)^1=1,040,604…年間運用益:1万303円
- 5年目:1,040,604×(1+0.01)^1=1,051,010…年間運用益:1万406円
複利の効果は運用年数が長いほど大きくなる
複利の特筆すべき特徴が、運用年数に伴って運用益が大きくなることです。5年くらいでは効果を実感しにくいですが、15年、20年、25年と、運用年数が長くなるほど運用益の増加幅は大きくなっていきます。
例えば、先ほど例に挙げた100万円を1%で運用した計算を、20年まで継続してみましょう
| 年数 | 元利合計 | 運用益合計 | 年間運用益 |
| 1年目 | 1,010,000 | 10,000 | 10,000 |
| 2年目 | 1,020,100 | 20,100 | 10,100 |
| 3年目 | 1,030,301 | 30,301 | 10,201 |
| 4年目 | 1,040,604 | 40,604 | 10,303 |
| 5年目 | 1,051,010 | 51,010 | 10,406 |
| 6年目 | 1,061,520 | 61,520 | 10,510 |
| 7年目 | 1,072,135 | 72,135 | 10,615 |
| 8年目 | 1,082,857 | 82,857 | 10,722 |
| 9年目 | 1,093,685 | 93,685 | 10,828 |
| 10年目 | 1,104,622 | 104,622 | 10,937 |
| 11年目 | 1,115,668 | 115,668 | 11,046 |
| 12年目 | 1,126,825 | 126,825 | 11,157 |
| 13年目 | 1,138,093 | 138,093 | 11,268 |
| 14年目 | 1,149,474 | 149,474 | 11,381 |
| 15年目 | 1,160,969 | 160,969 | 11,495 |
| 16年目 | 1,172,579 | 172,579 | 11,610 |
| 17年目 | 1,184,304 | 184,304 | 11,725 |
| 18年目 | 1,196,147 | 196,147 | 11,843 |
| 19年目 | 1,208,109 | 208,109 | 11,962 |
| 20年目 | 1,220,190 | 220,190 | 12,081 |
年を追うごとに年利率が高くなっているのがわかります。
これは、1%という低利率で計算したので、そこまで効果が大きくなりませんでしたが、同じく100万円を3%で複利運用したらどうでしょうか。
| 年数 | 元利合計 | 運用益合計 | 年間運用益 |
| 1年目 | 1,030,000 | 30,000 | 30,000 |
| 2年目 | 1,060,900 | 60,900 | 30,900 |
| 3年目 | 1,092,727 | 92,727 | 31,827 |
| 4年目 | 1,125,509 | 125,509 | 32,782 |
| 5年目 | 1,159,274 | 159,274 | 33,765 |
| 6年目 | 1,194,052 | 194,052 | 34,778 |
| 7年目 | 1,229,874 | 229,874 | 35,822 |
| 8年目 | 1,266,770 | 266,770 | 36,896 |
| 9年目 | 1,304,773 | 304,773 | 38,003 |
| 10年目 | 1,343,916 | 343,916 | 39,143 |
| 11年目 | 1,384,234 | 384,234 | 40,318 |
| 12年目 | 1,425,761 | 425,761 | 41,527 |
| 13年目 | 1,468,534 | 468,534 | 42,773 |
| 14年目 | 1,512,590 | 512,590 | 44,056 |
| 15年目 | 1,557,967 | 557,967 | 45,377 |
| 16年目 | 1,604,706 | 604,706 | 46,739 |
| 17年目 | 1,652,848 | 652,848 | 48,142 |
| 18年目 | 1,702,433 | 702,433 | 49,585 |
| 19年目 | 1,753,506 | 753,506 | 51,073 |
| 20年目 | 1,806,111 | 806,111 | 52,605 |
最初は年間3万円だった運用益が、11年目には4万円、19年目には5万円まで高くなりました。ちなみに、元本の額が増えても、年利率の増え方は変わりません。
エクセルで複利計算をする方法
複利運用の結果を算出するには、エクセルの活用が便利です。あらかじめ数式を入力しておけば、あとは元本を入力するだけで、運用年数に応じた結果をアウトプットしてくれます。
例えば、元本200万円を3%で複利運用するエクセルシートを作ってみましょう。
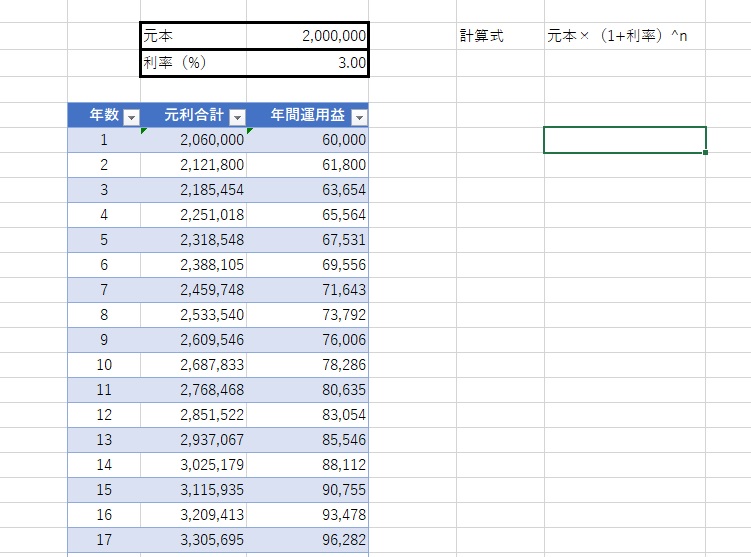
必要なのは、元本と利率のデータ、それと複利の計算式です。
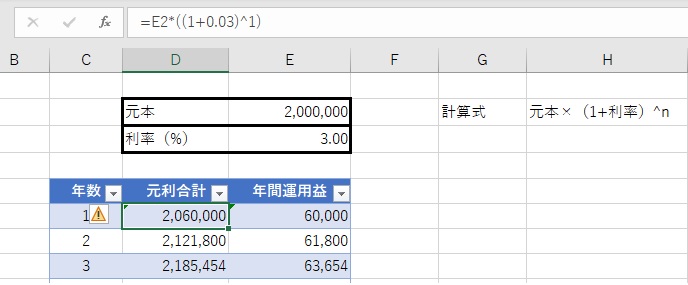
セルに直接複利の計算式を入力します。1年目は、元本を参照し、そこに3%の利率をかけます。計算式中では、利率の3%を0.03と表記します。これは直接入力するのがおすすめです。
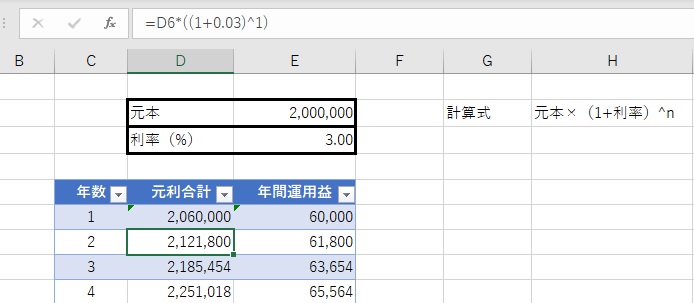
2年目以降は、前年の元利合計額を参照して、そこに3%の利率をかけます。以降目標年までこの式を用います。
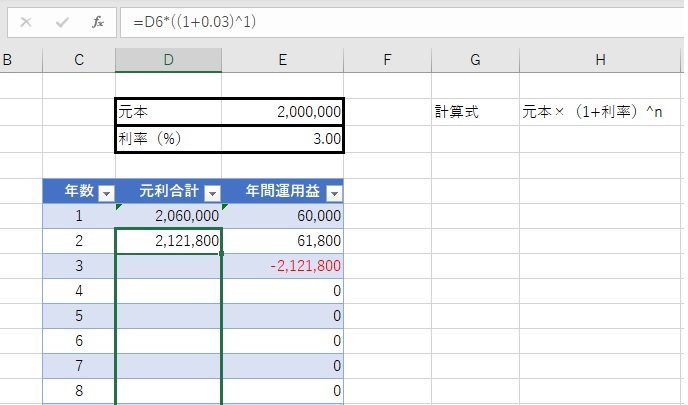
ちなみに、2年目のセルに数式を入力してしまえば、あとは数式のコピーでOKです。2年目のセルの右下に表示されていた四角い表示をつまんで、任意の場所までドラッグします。
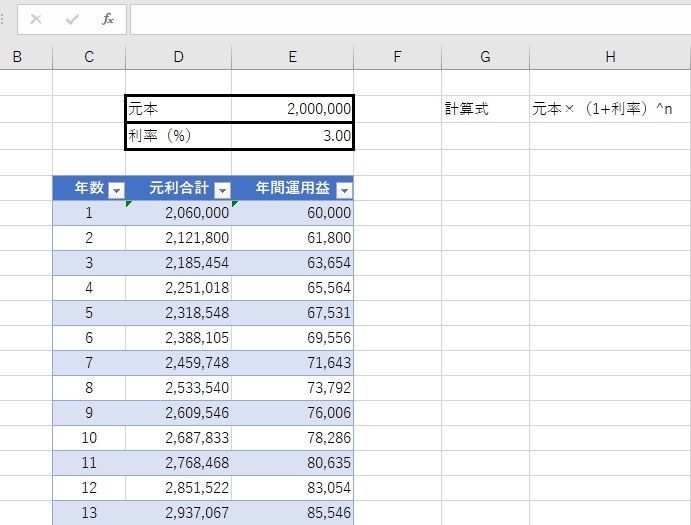
3年目以降のセルにも数式がコピーされ、各年の元利合計額が算出されました。なお、年間運用益の額は、当年の元利合計額から前年の元利合計額を差し引いて算出します。
以下に、今回複利計算用に作成したエクセルシートを添付しておきます。手早く複利計算をしたい方はこちらをご利用ください。
資産計画に重要な6つの係数を理解しよう
投資を計画的に行うためには、将来到達すると思われる額だけでなく、将来用意したい額のために必要な額や、いくらずつ積み立てていけばよいかなど、具体的な数値を求める必要があります。
これらの計算は手計算でも可能ですが、以下6つの係数を用いることで、より簡単に算出できます。
- 終価係数
- 現価係数
- 年金終価係数
- 減債基金係数
- 資本回収係数
- 年金現価係数
いずれも必要な係数は表にまとめられており、係数を求める計算は不要です。それぞれ詳しく見ていきましょう。
終価係数
終価係数とは、一定額の元本を複利運用した場合に、一定期間後に到達している額を求めるための係数です。つまり、先ほど紹介した複利計算を簡単に行うための係数ということです。
例えば元本100万円を5年間3%で運用した場合の額を求めるには、5年と3%の交わる箇所にある、1.159を100万に乗じて計算します。
計算例:元本100万円を5年間、年利3%で運用した場合
- 1,000,000×1.159=1,159,000円
| 1% | 2% | 3% | 4% | 5% | |
| 1年 | 1.010 | 1.020 | 1.030 | 1.040 | 1.050 |
| 2年 | 1.020 | 1.040 | 1.061 | 1.082 | 1.103 |
| 3年 | 1.030 | 1.061 | 1.093 | 1.125 | 1.158 |
| 4年 | 1.041 | 1.082 | 1.126 | 1.170 | 1.216 |
| 5年 | 1.051 | 1.104 | 1.159 | 1.217 | 1.276 |
| 6年 | 1.062 | 1.126 | 1.194 | 1.265 | 1.340 |
| 7年 | 1.072 | 1.149 | 1.230 | 1.316 | 1.407 |
| 8年 | 1.083 | 1.172 | 1.267 | 1.369 | 1.477 |
| 9年 | 1.094 | 1.195 | 1.305 | 1.423 | 1.551 |
| 10年 | 1.105 | 1.219 | 1.344 | 1.480 | 1.629 |
| 11年 | 1.116 | 1.243 | 1.384 | 1.539 | 1.710 |
| 12年 | 1.127 | 1.268 | 1.426 | 1.601 | 1.796 |
| 13年 | 1.138 | 1.294 | 1.469 | 1.665 | 1.886 |
| 14年 | 1.149 | 1.319 | 1.513 | 1.732 | 1.980 |
| 15年 | 1.161 | 1.346 | 1.558 | 1.801 | 2.079 |
| 16年 | 1.173 | 1.373 | 1.605 | 1.873 | 2.183 |
| 17年 | 1.184 | 1.400 | 1.653 | 1.948 | 2.292 |
| 18年 | 1.196 | 1.428 | 1.702 | 2.026 | 2.407 |
| 19年 | 1.208 | 1.457 | 1.754 | 2.107 | 2.527 |
| 20年 | 1.220 | 1.486 | 1.806 | 2.191 | 2.653 |
現価係数
現価係数とは、一定期間後に一定額を用意するための元本を求める係数です。例えば、年利5%で運用して、5年後に200万円を用意するための元本を求めるには、200万円に、5年と5%の交差するところの0.784を乗じて求めます。
計算例:年利5%で運用して、5年後に200万円を用意するための元本
- 2,000,000×0.784=1,568,000円
| 1% | 2% | 3% | 4% | 5% | |
| 1年 | 0.990 | 0.980 | 0.971 | 0.962 | 0.952 |
| 2年 | 0.980 | 0.961 | 0.943 | 0.925 | 0.907 |
| 3年 | 0.971 | 0.942 | 0.915 | 0.889 | 0.864 |
| 4年 | 0.961 | 0.924 | 0.888 | 0.855 | 0.823 |
| 5年 | 0.951 | 0.906 | 0.863 | 0.822 | 0.784 |
| 6年 | 0.942 | 0.888 | 0.837 | 0.790 | 0.746 |
| 7年 | 0.933 | 0.871 | 0.813 | 0.760 | 0.711 |
| 8年 | 0.923 | 0.853 | 0.789 | 0.731 | 0.677 |
| 9年 | 0.914 | 0.837 | 0.766 | 0.703 | 0.645 |
| 10年 | 0.905 | 0.820 | 0.744 | 0.676 | 0.614 |
| 11年 | 0.896 | 0.804 | 0.722 | 0.650 | 0.585 |
| 12年 | 0.887 | 0.788 | 0.701 | 0.625 | 0.557 |
| 13年 | 0.879 | 0.773 | 0.681 | 0.601 | 0.530 |
| 14年 | 0.870 | 0.758 | 0.661 | 0.577 | 0.505 |
| 15年 | 0.861 | 0.743 | 0.642 | 0.555 | 0.481 |
| 16年 | 0.853 | 0.728 | 0.623 | 0.534 | 0.458 |
| 17年 | 0.844 | 0.714 | 0.605 | 0.513 | 0.436 |
| 18年 | 0.836 | 0.700 | 0.587 | 0.494 | 0.416 |
| 19年 | 0.828 | 0.686 | 0.570 | 0.475 | 0.396 |
| 20年 | 0.820 | 0.673 | 0.554 | 0.456 | 0.377 |
年金終価係数
年金終価係数とは、一定額を積み立てていった場合の、一定期間後の元利合計額を求める係数です。例えば、毎年20万円を年利3%で積み立てていって、10年後にいくらになっているかを求める場合は、20万円に10年と3%が交差するところの11.464を乗じて求めます。
計算例:毎年20万円を年利3%で積み立てた場合の10年後の額
- 200,000×11.646=2,329,200円
| 1% | 2% | 3% | 4% | 5% | |
| 1年 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 2年 | 2.010 | 2.020 | 2.030 | 2.040 | 2.050 |
| 3年 | 3.030 | 3.060 | 3.091 | 3.122 | 3.153 |
| 4年 | 4.060 | 4.122 | 4.184 | 4.246 | 4.310 |
| 5年 | 5.101 | 5.204 | 5.309 | 5.416 | 5.526 |
| 6年 | 6.152 | 6.308 | 6.468 | 6.633 | 6.802 |
| 7年 | 7.214 | 7.434 | 7.662 | 7.898 | 8.142 |
| 8年 | 8.286 | 8.583 | 8.892 | 9.214 | 9.549 |
| 9年 | 9.369 | 9.755 | 10.159 | 10.583 | 11.027 |
| 10年 | 10.462 | 10.950 | 11.464 | 12.006 | 12.578 |
| 11年 | 11.567 | 12.169 | 12.808 | 13.486 | 14.207 |
| 12年 | 12.683 | 13.412 | 14.192 | 15.026 | 15.917 |
| 13年 | 13.809 | 14.680 | 15.618 | 16.627 | 17.713 |
| 14年 | 14.947 | 15.974 | 17.086 | 18.292 | 19.599 |
| 15年 | 16.097 | 17.293 | 18.599 | 20.024 | 21.579 |
| 16年 | 17.258 | 18.639 | 20.157 | 21.825 | 23.657 |
| 17年 | 18.430 | 20.012 | 21.762 | 23.698 | 25.840 |
| 18年 | 19.615 | 21.412 | 23.414 | 25.645 | 28.132 |
| 19年 | 20.811 | 22.841 | 25.117 | 27.671 | 30.539 |
| 20年 | 22.019 | 24.297 | 26.870 | 29.778 | 33.066 |
減債基金係数
減債基金係数とは、一定期間後に一定額を用意するために毎年積み立てる額を求めるための係数です。例えば、10年後に100万円を用意するために毎年一定額を積み立てる場合、5%運用をした場合に積み立てるべき額は、100万円に、10年と5%の交わる0.080を乗じて求めます。
計算例:10年後に100万円を用意するために、年利5%で運用しながら積み立てた場合、毎年いくら積み立てればよいか
- 1,000,000×0.080=80,000円
| 1% | 2% | 3% | 4% | 5% | |
| 1年 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 2年 | 0.498 | 0.495 | 0.493 | 0.490 | 0.488 |
| 3年 | 0.330 | 0.327 | 0.324 | 0.320 | 0.317 |
| 4年 | 0.246 | 0.243 | 0.239 | 0.235 | 0.232 |
| 5年 | 0.196 | 0.192 | 0.188 | 0.185 | 0.181 |
| 6年 | 0.163 | 0.159 | 0.155 | 0.151 | 0.147 |
| 7年 | 0.139 | 0.135 | 0.131 | 0.127 | 0.123 |
| 8年 | 0.121 | 0.117 | 0.112 | 0.109 | 0.105 |
| 9年 | 0.107 | 0.103 | 0.098 | 0.094 | 0.091 |
| 10年 | 0.096 | 0.091 | 0.087 | 0.083 | 0.080 |
| 11年 | 0.086 | 0.082 | 0.078 | 0.074 | 0.070 |
| 12年 | 0.079 | 0.075 | 0.070 | 0.067 | 0.063 |
| 13年 | 0.072 | 0.068 | 0.064 | 0.060 | 0.056 |
| 14年 | 0.067 | 0.063 | 0.059 | 0.055 | 0.051 |
| 15年 | 0.062 | 0.058 | 0.054 | 0.050 | 0.046 |
| 16年 | 0.058 | 0.054 | 0.050 | 0.046 | 0.042 |
| 17年 | 0.054 | 0.050 | 0.046 | 0.042 | 0.039 |
| 18年 | 0.051 | 0.047 | 0.043 | 0.039 | 0.036 |
| 19年 | 0.048 | 0.044 | 0.040 | 0.036 | 0.033 |
| 20年 | 0.045 | 0.041 | 0.037 | 0.034 | 0.030 |
資本回収係数
資本改修係数とは、一定額を一定期間で取り崩した場合に、毎年受け取れる額を求める係数です。例えば、100万円を年利3%で運用しながら、5年間にわたって受け取れる額を求める場合、100万に、5年と3%が交わるところの0.218を乗じて求めます。
計算例:100万円を年利3%で運用しながら5年にわたって受け取った場合の1年あたりの額
- 1,000,000×0.218=218,000円
| 1% | 2% | 3% | 4% | 5% | |
| 1年 | 1.010 | 1.020 | 1.030 | 1.040 | 1.050 |
| 2年 | 0.508 | 0.515 | 0.523 | 0.530 | 0.538 |
| 3年 | 0.340 | 0.347 | 0.354 | 0.360 | 0.367 |
| 4年 | 0.256 | 0.263 | 0.269 | 0.275 | 0.282 |
| 5年 | 0.206 | 0.212 | 0.218 | 0.225 | 0.231 |
| 6年 | 0.173 | 0.179 | 0.185 | 0.191 | 0.197 |
| 7年 | 0.149 | 0.155 | 0.161 | 0.167 | 0.173 |
| 8年 | 0.131 | 0.137 | 0.142 | 0.149 | 0.155 |
| 9年 | 0.117 | 0.123 | 0.128 | 0.134 | 0.141 |
| 10年 | 0.106 | 0.111 | 0.117 | 0.123 | 0.130 |
| 11年 | 0.096 | 0.102 | 0.108 | 0.114 | 0.120 |
| 12年 | 0.089 | 0.095 | 0.100 | 0.107 | 0.113 |
| 13年 | 0.082 | 0.088 | 0.094 | 0.100 | 0.106 |
| 14年 | 0.077 | 0.083 | 0.089 | 0.095 | 0.101 |
| 15年 | 0.072 | 0.078 | 0.084 | 0.090 | 0.096 |
| 16年 | 0.068 | 0.074 | 0.080 | 0.086 | 0.092 |
| 17年 | 0.064 | 0.070 | 0.076 | 0.082 | 0.089 |
| 18年 | 0.061 | 0.067 | 0.073 | 0.079 | 0.086 |
| 19年 | 0.058 | 0.064 | 0.070 | 0.076 | 0.083 |
| 20年 | 0.055 | 0.061 | 0.067 | 0.074 | 0.080 |
年金現価係数
年金現価係数とは、一定期間にわたって一定額を受け取るための元本を求める係数です。例えば、5年間にわたって20万円ずつ受け取りたい場合、年利3%で運用した場合に必要な元本は、20万に、5年と3%が交差するところの4.580を乗じて求めます。
計算例:5年間にわたって20万円ずつ受け取りたい場合に、年利3%で運用した場合に必要な元本
- 200,000×4.580=916,000円
| 1% | 2% | 3% | 4% | 5% | |
| 1年 | 0.990 | 0.980 | 0.971 | 0.962 | 0.952 |
| 2年 | 1.970 | 1.942 | 1.913 | 1.886 | 1.859 |
| 3年 | 2.941 | 2.884 | 2.829 | 2.775 | 2.723 |
| 4年 | 3.902 | 3.808 | 3.717 | 3.630 | 3.546 |
| 5年 | 4.853 | 4.713 | 4.580 | 4.452 | 4.329 |
| 6年 | 5.795 | 5.601 | 5.417 | 5.242 | 5.076 |
| 7年 | 6.728 | 6.472 | 6.230 | 6.002 | 5.786 |
| 8年 | 7.652 | 7.325 | 7.020 | 6.733 | 6.463 |
| 9年 | 8.566 | 8.162 | 7.786 | 7.435 | 7.108 |
| 10年 | 9.471 | 8.983 | 8.530 | 8.111 | 7.722 |
| 11年 | 10.368 | 9.787 | 9.253 | 8.760 | 8.306 |
| 12年 | 11.255 | 10.575 | 9.954 | 9.385 | 8.863 |
| 13年 | 12.134 | 11.348 | 10.635 | 9.986 | 9.394 |
| 14年 | 13.004 | 12.106 | 11.296 | 10.563 | 9.899 |
| 15年 | 13.865 | 12.849 | 11.938 | 11.118 | 10.380 |
| 16年 | 14.718 | 13.578 | 12.561 | 11.652 | 10.838 |
| 17年 | 15.562 | 14.292 | 13.166 | 12.166 | 11.274 |
| 18年 | 16.398 | 14.992 | 13.754 | 12.659 | 11.690 |
| 19年 | 17.226 | 15.678 | 14.324 | 13.134 | 12.085 |
| 20年 | 18.046 | 16.351 | 14.877 | 13.590 | 12.462 |
取引のシミュレーションには投資ゲームが便利
金額の見通しだけでなく、市場の値動きや社会情勢などを踏まえた、実践的なシミュレーションをしたい場合は、デモトレードができる投資ゲームが便利です。
ゲームといえど、本物さながらの環境でプレイできるものも多く、実際の上場銘柄やリアルタイムチャートを使っているものも多いです。初心者が取引の感覚を学ぶのに便利なだけでなく、ノーリスクで投資を試せる、分析用ツールとしても役立ちます。
有名なアプリとしては、株たすやトウシカ、moomooなどがあります。
まずは実際に計算してみるところから始めよう
今回は、複利運用の基本から計算方法、資産計画に便利な6つの係数について解説しました。いずれも投資のシミュレーションに必要不可欠な要素なので、基礎知識としてしっかり覚えておきましょう。
計算は実際に触れてみないとなかなか覚えられないものです。まずは大雑把でよいので、将来の目標額を決め、必要な元本や運用する場合の利率などを算出してみましょう。
何事でも、自分事として具体的に考えると実感がわいてくるものです。投資を始める第一歩として、計算に取り組んでみてはいかがでしょうか。
弊社横浜のFPオフィス「あしたば」は、創業当初からNISA・ジュニアNISAやiDeCo/イデコ・企業型確定供出年金(DC/401k)のサポートに力を入れています。
収入・資産状況や考え方など人それぞれの状況やニーズに応じた「具体的なNISAやiDeCoの活用法と注意点」から「バランスのとれたプランの立て方」まで、ファイナンシャルプランナーがしっかりとアドバイスいたしますので、ぜひお気軽にご相談ください。
大好評の「無料オンラインセミナー」も随時開催中!
↓↓↓弊社推奨の「低コストiDeCo加入窓口」はこちら↓↓↓
























